Výpočtom veľkosti sekundárneho zrkadla sa venovalo mnoho článkov a autorov. Existujú programy (Newt, Newton, …) ktoré okrem výpočtu veľkosti zrkadla dokážu určiť mnoho ďalších parametrov. Pretože článkov v Slovenskom alebo Českom jazyku je veľmi málo (napríklad články Milana Kamenického v Kozmose) a existuje mnoho astronómov, ktorí neovládajú anglický jazyk na dostatočnej úrovni, rozhodol som sa napísať tento článok.Newtonov ďalekohľad patrí medzi jednoduché optické prístroje. Jeho plnohodnotný výkon závisí od niekoľkých parametrov a jedným z nich je aj správna veľkosť sekundárneho zrkadla. Ak by bolo sekundárne zrkadlo malé, nedokázalo by vykresliť dostatočne osvetlené zorné pole. Ak bude zrkadlo naopak príliš veľké, spôsobovalo by veľké ohybové javy. Jeho plocha by uberala využiteľnú plochu primárneho zrkadla a degradovala by tak ďalekohľad.

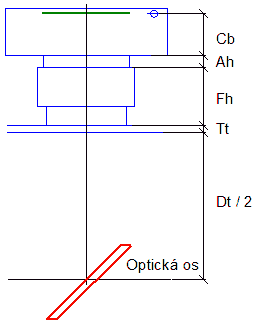
Určenie veľkosti sekundáru nie je vo svojej podstate veľmi zložité. Postačia jednoduché matematické operácie, prípadne kresba sústavy v mierke. Začnime určením dĺžky svetelného kužeľa medzi sekundárom a ohniskovou rovinou (inak povedané vzdialenosťou ohniskovej roviny od optickej osi). Táto vzdialenosť je určená použitým okulárovým výťahom a napríklad aj použitím ďalekohľadu. Ak chceme ďalekohľad na vizuálne pozorovanie, postačí spravidla k výške zasunutého okulárového výťahu pripočítať 10 – 12mm. Ak však chceme fotografovať v primárnom ohnisku, je potrebné pripočítať aj vzdialenosť od prednej steny fotoaparátu po rovinu filmu. Pozrime sa na okulárovú časť bližšie.

Dt – vnútorný priemer tubusu Tt – hrúbka steny tubusu Fh – výška zasunutého okulárového výťahu Ah – hrúbka koncovky na pripojenie fotoaparátu (napríklad T2 adaptér) Cb – hĺbka tela fotoaparátu po rovinu filmu s – vzdialenosť ohniskovej roviny od optickej osi

potom


s = Dt/2 + Tt + Fh + Ah + Cb


Pozrime sa na celkovú schému ďalekohľadu, do ktorého vstupujú paralelné lúče.


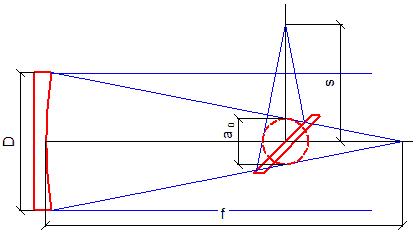
D - priemer primárneho zrkadla
f - ohnisková vzdialenosť primárneho zrkadla
s - vzdialenosť ohniskovej roviny od optickej osi (tak ako sme ju určili vyššie)
a0 - minimálny rozmer malej osi sekundárneho zrkadla

z podobnosti trojuholníkov vyplýva, že:

a0/D = s/F
a0 = D * s/F

Takto veľké sekundárne zrkadlo však bude zobrazovať obraz, ktorého jasnosť bude prudko klesať k okraju. V skutočnosti potrebujeme 100% osvetlenie zorného poľa istej (nenulovej) veľkosti. Potrebujeme zrkadlo väčšie ako už vypočítané minimálne. Aké teda má byť 100% osvetlené zorné pole?

1. Ak ide o ďalekohľad na všeobecné vizuálne pozorovanie, potrebujeme zorné pole aspoň 0.5° – 1°.
2. V prípade využitia na pozorovanie planét postačí vzhľadom na uhlové rozmery planét menšie zorné pole (0.25°).

Pozrime sa teda na schému ďalekohľadu, keď vstupujúce lúče zvierajú uhol vykresleného zorného poľa.


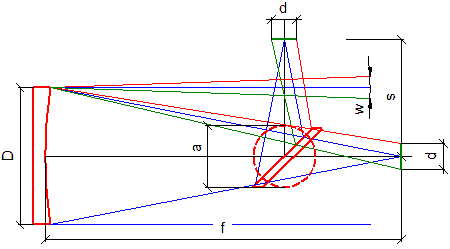
D - priemer primárneho zrkadla
f - ohnisková vzdialenosť primárneho zrkadla
s - vzdialenosť ohniskovej roviny od optickej osi (tak ako sme ju určili vyššie)
a - rozmer malej osi sekundárneho zrkadla
w - uhlová veľkosť zorného poľa
d - veľkosť 100% osvetleného zorného poľa

Najprv teda zistime veľkosť zorného poľa aby sme mohli vypočítať malú os sekundárneho zrkadla. Uhol w je malý, a preto platí vzťah.

(1/2 * d)/f = sin(w/2)
d/2 = f * sin(w/2)
d = 2 * f * sin(w/2)

Ak sa jedná o fotografický ďalekohľad, veľkosť zorného poľa určujeme z rozmeru obrazového snímača. Nemusí to byť totiž len film ale aj rôzne druhy (a rozmery) CCD prvkov. Napríklad na kinofilmové políčko by sme mali uvažovať aspoň 20mm zorné pole. Na zvyšku políčka síce bude klesať jasnosť obrazu ale v prípade filmového materiálu to dokáže do istej miery vykompenzovať pružnosť. V prípade CCD snímačov je možné nerovnomerne osvetlené zorné pole vykompenzovať digitálnym spracovaním.

Z nasledovnej schémy je zrejmé ako sa dá získať vzťah pre veľkosť malej osi sekundárneho zrkadla.


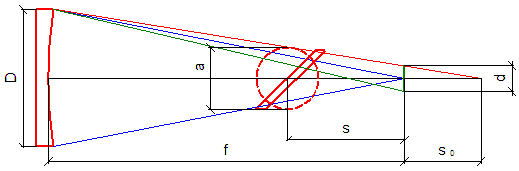
D - priemer primárneho zrkadla
f - ohnisková vzdialenosť primárneho zrkadla
s - vzdialenosť ohniskovej roviny od optickej osi (po otočení o 90° od osi sekundárneho zrkadla)
a - rozmer malej osi sekundárneho zrkadla
d - rozmer 100% osvetleného zorného poľa
s0 - vzdialenosť priesečníka okrajového lúča a optickej osi od ohniskovej roviny

Z podobnosti trojuholníkov vyplývajú vzťahy:

po spojení oboch vzťahov

(d * f)/(D - d) = (s * d)/(a - d)
f/(D - d) = s/(a - d)
f * (a - d) = s * (D - d)
a - d = (s * (D - d))/f
a = ((s * (D - d))/f) + d

Poznáme teda veľkosť malej osi sekundárneho zrkadla. Pozrime sa teraz na sekundárne zrkadlo.

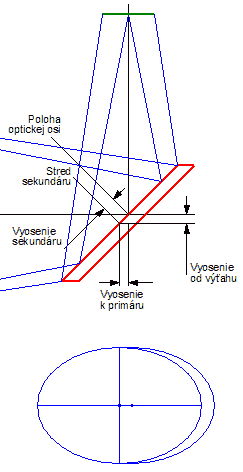
Všimnime si, že pri veľkej svetelnosti primárneho zrkadla neleží sekundárne zrkadlo celou svojou plochou v ceste svetelného kužeľa. Je potrebné vyosiť sekundárne zrkadlo – posunúť jeho stred pod optickú os primárneho zrkadla. Niekomu sa môže zdať vyosenie zbytočné. Je však treba si uvedomiť, že ak bude sekundárne zrkadlo umiestnené svojou osou na optickej osi jeho časť bude nevyužitá, ohybové obrazy hviezd budú deformované a stred osvetleného zorného poľa bude posunutý mimo optickú os. Vezmime si na porovnanie extrémny príklad. Pre 50cm zrkadlo svetelnosti 1:5 a sekundárne zrkadlo dostatočne veľké na osvetlenie 20mm zorného poľa je vyosenie približne 5mm. Voči veľkosti sekundárneho zrkadla je to zdanlivo málo. Ak ale zrkadlo nevyosíme, bude stred 100% osvetleného poľa posunutý 5mm k primárnemu zrkadlu. Ako teda zistiť veľkosť vyosenia sekundárneho zrkadla? Vezmime si z predchádzajúcich schém nasledovné hodnoty.

D - priemer primárneho zrkadla
f - ohnisková vzdialenosť primárneho zrkadla
t - prehĺbenie paraboloidu
s - vzdialenosť ohniskovej roviny od optickej osi
d - rozmer 100% osvetleného zorného poľa

Pre prehĺbenie paraboloidu platí:

t = D2/(16 * f)

Pre veľkosť vyosenia v smere od okulárového výťahu platí:

v = (L/M - L/N)/2

Pomocné premenné L, M a N sú definované nasledovne:

L = d * (f - t) + s * (D - d)
M = 2 * (f - t) - D + d
N = 2 * (f - t) + D - d


Dúfam, že informácie pomohli pri určení tej správnej veľkosti zrkadla. Na analýzu sekundárneho zrkadla možno použiť pripravený interaktívny formulár. Výpočet ukáže aj pokles osvetlenia a stratu v magnitúdach s rastúcou plochou zorného poľa.